The Average Number of Starters Over Time
For the foreseeable future my work will focus on understanding how specific game situations affect team, unit, and player performance. The end goal is to understand what performance in these specific situations means with respect to true player ability.
To kick this off, I’ve decided to take a very general look at how the average number of starters changes over elapsed game time. First, however, I’ll present the work of another:
Previous Work
Earlier this year, Ben F. over at the APBRmetrics forum created a post called Fun With Charts: Sub Patterns. In this post, Ben linked to a neat tool he created with Open Flash Chart: League Substitution Patterns
This is a pretty cool tool that allows you to see how each team (and their opponents) substitution patterns match up with the league average. I, however, want to take a step back from this level of detail and incorporate the difference between the substitution patterns of home and away teams. Therefore, I am not going to worry about the team variation aspect at this time.
My Idea
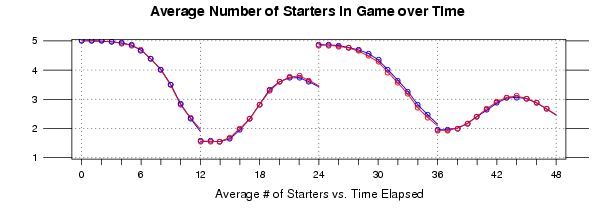
I really like Ben’s tool, but I want to see how the average team varies over elapsed game time at home and on the road. To do this, I extracted the average number of starters league wide from the 2007-2008 regular season play-by-play data.
The results are summarized by the following graph:
Click Image for Full Size
First I will explain what you see in the graph above. The y-axis, from 5 to 1, is the average number of starters in the game at a given time in the game. The x-axis, from 0 to 48, is the elapsed game time. The blue dots and lines represent the home team, and the red dots and lines represent the away team.
The points represent times at which the data was captured for. The lines are drawn from smoothing splines that I fit with R for each team during each quarter.
Things to Take from This
The first thing I noticed in the data is that there does not appear to be a big difference between the substitution patterns of home versus road teams. This surprised me, but it is actually nice to know that sub patterns can’t explain much of the home court advantage. I will need to look elsewhere for that.
Also, it is interesting to notice the difference between the curves of the data from each quarter. The 1st and 3rd quarters are fairly similar in shape, but the 2nd and 4th quarters have some distinct shapes.
Reproduce These Results
In this archive you will find the data and R code I used to create the graph above and the smoothing splines fit to the data.
To run the code: extract the archive, open R, and run: source(“starters.R”)
The Next Step
Now that we’ve got a basic idea of how the average number of starters varies over time, the next step is to look at how the average number of starters changes based on the game’s point differential. After that, I will try to model how the average number of starters changes based on the game’s elapsed time and point differential.
Welcome ESPN The Magazine Readers
Let me first welcome you to the website. The about page and my welcome post will help bring you up to speed on who I am and why I’ve created this website. You can also checkout the archives to see what I’ve posted since the inception of this website. If you’re interested in keeping up with the website, you can subscribe to updates for free by e-mail or RSS.
I suspect that you are like most people and are not up to date with the latest in basketball research. Therefore, I’m writing this post to bridge this knowledge gap. Make sure you read from start to end, as this will allow you to score a few nerd points.
Why Am I Here?
I’ll assume you’re lazy like me and didn’t click through to my about page or the welcome post that I linked above. If you’re still too lazy to take a look, here is a short list of things that drive my desire to grow this website:
- To create and share better models of basketball
- To provide an open source of data for independent and reproducible research
- To increase the data tracked to improve our understanding of the game (see my defensive project for the 2008-2009 regular season as an example)
I envy baseball. Not the excitement of the game compared to basketball, but the community they have developed and the open share of information available for research.
Everyday I wake up and hope someone has put together a retrosheet for basketball and the NBA has provided an XML feed for the shot trajectories of every shot taken (see MLB’s PitchFX).
These things haven’t happened yet, but I want to push basketball into this direction. The data I am compiling and making available has really one major goal: to simplify the data gathering process for basketball research. Basketball Value has paved the way for providing similar data for some time now, but I would like to make the task of assembling data from these data sets much easier.
The State of Basketball Research
Basketball research has come a long way since Dean Oliver created the Journal of Basketball Studies way back when in the 90s. To give this some perspective, I was a pre-teen during this time doing what every other 12 year old basketball fan was doing: trying to become Michael Jordan. Oh, and in case you were wondering, this didn’t work out for me and many others like me.
So clearly this was a long time ago, but we’ve come a long way since then. Dean’s book Basketball on Paper (BoP) helped lay the foundation for the way we look at basketball in a tempo-free manner. There is plenty of credit to be given out for bringing us to where we are today, but BoP helped fuel my interest, so I’m going to give Dean most of the credit. Sorry everyone else.
The Best Forum on the Web
The basketball analytics community hangs out at a placed called the APBRmetrics forum. This is where you’ll find the ever growing community of basketball geeks. Make sure you register for an account to join the discussion.
Other Great Sites
If you’re looking for more to read, make sure you also checkout these websites:
Thanks For Stopping By
So there you have it. You’ll have way more street cred after you’ve become familiar with all of the resources linked in this post.
If you’ve made it this far without passing out, make sure to subscribe to updates, as I suspect you just might be interested in reading future basketball research I post.
2007-2008 Regular Season Play-By-Play Data Now Available
I want to let everyone know that I’ve updated the data page with an initial draft of the 2007-2008 regular season play-by-play data.
This data is in CSV format, and includes every player on the court along with any shot location information available.
To provide this data in this format, I haven’t been able to make a comprehensive archive. As of now I’m missing 47 games, or about 3.8% of the games. About 35 or so of these games I believe I can provide at some point, but it involves trying to figure out who is on the court by hand (my programs can only do so much). If you need any of these games, give Basketball Value a shot.
Here is the direct download link:
http://www.basketballgeek.com/downloads/2007-2008.regular_season.zip
Let me know of any failures (and successes!) you have with this data set.
Getting Defensive for the 2008-2009 Regular Season
Now that I have a theoretical model for the probability of winning a basketball game, my goal is to collect data that will help make a useful practical model for the probability of winning a basketball game.
Existing Data
There is a lot of existing data to examine for contribution to a useful practical model for the probability of winning a basketball game. Not only that, but I expect a lot of this data to be useful. That said, this data set is far from complete with respect to its representation of the game of basketball. My goal is to add a small supplement to what the league is currently collecting to aid in understanding.
As of now, the largest need for improved data collection is with respect to defense. Therefore, this is the area that I will be focusing my data collection efforts on.
My Playoff Experiment
For the 2008 playoffs, I experimented with tracking a lot of data. Thanks in large part to the theoretical model and useful input from the analytic community, I will be focusing my efforts on collecting data that will have a direct impact on a practical model for the probability of winning a basketball game. Therefore, while some of the data I was collecting would be nice to have, this defensive data is the most important for the model I want to build.
Tracking Defenders
Although things like potential assists and pick assists are useful to know, they really only impact the defensive state a player is facing when they take a shot. This means my focus is on tracking this defensive state instead of trying to keep track of the numerous ways teammates help create spacing on offense.
The Importance of Defensive State
Although this may seem fairly basic, I feel strongly that tracking defenders that contest shots will add a lot to existing data.
Gaining more insight into team defense, especially as it relates to players and strategy, should prove to be worthwhile. Also, the goal is to use some statistical techniques to gain insight into defense without having actually tracked the data. This means we will be able to use things like play-by-play approximate these defensive states based on the sample of data that actually gets collected.
Interested In Tracking Data?
I can’t track every game. I would like to, but it’s not feasible for me. If I tried, numerous bad things would happen to me. My wife would leave me, my dogs would go hungry, and I’d fail out of school. Clearly this is not the optimal way to spend my time.
That said, I plan on making the data collection process as painless as possible to encourage others to help. Therefore, if you have a DVR and would like to help collect this defensive data, please e-mail me at: ryan@basketballgeek.com.
A Theoretical Model for The Probability of Winning a Basketball Game – Part 3
This is the third in a 3 part series where I will present a theoretical model for the probability of winning a basketball game. The 3 parts will break this model down at the team, unit, and player level.
In part two of this series I presented a way to break down the probability of winning a basketball game from the points scored per 5-player unit per play to the actual players themselves.
At the end of part two, I finished the post with the following formula:
E(Points) = Pr(O1) x E(Points | O1) + Pr(O2) x E(Points | O2) + Pr(O3) x E(Points | O3)
+ Pr(O4) x E(Points | O4) + Pr(O5) x E(Points | O5)
This formula is how I’ve chosen to break down the points scored per 5-player unit per play into the player-level components.
The Components of This Formula for E(Points)
Specifying E(Points) in this way allows us to understand how each player impacts the expectation at the 5-player unit level, which in turn affects the team’s probability of winning.
In this formula Pr(OX) represents the probability that offensive player X is responsible for the event that leads to the end of the play. Referring to the 5-player unit level, this is an event such as a field goal attempt, turnover, etc. Clearly Pr(O1) + Pr(O2) + Pr(O3) + Pr(O4) + Pr(O5) must be equal to 1.
What Affects Pr(OX)?
One of the most important pieces of this formula is how Pr(OX) is constructed. First, I’ll start with a quick list of things that affect a player’s probability of using any given play (that’s what I’m calling Pr(OX), for those of you that fell asleep during the last section):
- Game situation
- Fatigue
- Focus
Game situation affects the offensive and defensive team’s priorities. Thus any given player’s role within that context will change, hence changing Pr(OX) for every player. Fatigue is what I will refer to as each player’s physical state, and focus is what I will refer to as each player’s mental state. The offensive and defensive player’s fatigue and focus will also affect Pr(OX). It’s worth pointing out that game situation can affect focus, so these are certainly not independent factors.
Breaking Down E(Points | OX)
Now that we know what will affect Pr(OX), lets now derive what E(Points | OX) looks like. To prevent redundancy, I won’t bother to re-define the specific player level pieces of E(Points), as it is very similar to the breakdown at the 5-player unit level that started off with the definition of:
E(Points) = Pr(No Turnover) x E(Points | No Turnover)
+ Pr(Turnover) x E(Points | Turnover)
Instead of regurgitating the list of possibilities given specific shots with or without a shooting foul, I will focus on plays that lead directly to points. The rates of events like turnovers will increase with lower levels of fatigue and focus, but hopefully that is obvious.
Focusing on Point Producing Events
Every shooting event can be broken down into the following:
E(Points) = Pr(No Shooting Foul) x E(Points | No Shooting Foul)
+ Pr(Shooting Foul) x E(Points | Shooting Foul)
So if we know player X takes a shot, we know that some percentage of the time they are not fouled, and some percentage of the time they are fouled.
Shots Without a Foul
First lets examine E(Points | No Shooting Foul), the expected points for a shot given a shooting foul did not take place. For any given shot, E(Points) is given by:
E(Points) = Pr(Make) x E(Points | Make) + Pr(Miss) x 0
Because E(Points | Make) can only be 2 or 3 points (depending on the shot type), we simply need to focus on the probability Pr(Make).
Pr(Make) is affected by the same factors as Pr(OX). We can go a little further, though, and say that a player’s Pr(Make) for a shot is really conditional on these factors at the time of the shot, and can be written as:
Pr(Make) = Pr(Make | Shot Location, Own Fatigue, Own Focus, Opponent State)
In words, this means that a player’s probability of making a shot is conditional on the shot location, the player’s fatigue and focus, and the opponent state. For clarity, opponent state signifies the defensive pressure on the shot attempt.
Trying to understand the structure of how the shot location, own fatigue and focus, and opponent state is more of a practical model issue, as in “How would we create a model to generate a probability when we take these factors into account?”. It’s certainly something I think about often, and I would be lying if I had the perfect model in mind. Hopefully this will evolve over time as I work to construct these models.
Shots With a Foul
For completeness, I will make a comment about shots with a foul. Shots that have a foul really only change the opponent state in the specification of a shot without a foul given above. Clearly Pr(Make) will decrease in this situation. How we model this is again a practical issue.
The Next Step
The next step is to start building practical models of the pieces derived in this theoretical picture of the probability of winning a basketball game. As I build these practical pieces, the plan is to make assumptions about the missing components and work with the pieces I’ve got to create more important questions and generate new insight about what a good practical model for the probability of winning a basketball game looks like.
Overall I feel this is a good theoretical model to start with. It’s not perfect, it doesn’t capture everything, but it seems to capture the important stuff. If you made it through all 3 parts of this series, thanks for hanging in there with me! This isn’t the most entertaining aspect of this work, but (for me, at least) it helps focus future effort, which is very valuable.