Estimating the Impact of Aging on 3FG%
- 884 Comment
The impact of aging on player performance interests me, but I haven’t really done anything useful in this area. Baseball’s recent debate (really fantastic stuff) on the topic of player aging curves has motivated me to take a closer look at the affect of aging on 3pt shooting.
Ed Küpfer’s three year old post on aging is the best resource I know of on the topic, but I’m sure he’s got something more useful than what’s in that post. That said, I’d like to specifically estimate an aging curve for the 3pt shooting abilities of NBA players.
The Data
Using Basketball-Reference.com‘s excellent Player Season Finder, I collected 3pt shooting data for players that attempted at least two 3pt shots during any season from 1999-00 to 2008-09. This resulted in a data set containing a little over 3300 player seasons.
The Model
Individual 3pt shooting performance is more than a function of player ability and age, but in this case I’m specifically interested in estimating the affect of age. Further, I would like to estimate an aging curve for each player under the assumption that each player has their own unique aging curve.
To do this, I’ve chosen to use a multilevel model that allows the intercept and slope to vary by player, as this model allows for the estimation of a unique aging curve for each player. The aging curve is assumed to be of the form [latex]\alpha + \beta_{0}(age) + \beta_{1}(age^{2})[/latex].
The Results
The model fit estimates the the average player’s peak age in 3pt shooting ability is 29, and the p-values for the [latex]\beta_{0}[/latex] and [latex]\beta_{1}[/latex] coefficients in the model form listed above are both less than 0.01.
The estimates for each player are listed in the following spreadsheet: 3FG% Aging Estimates
In this spreadsheet you will find each player’s estimated peak age along with 3FG% estimates for each player from age 20 to 40.
With the exception of Andre Miller, most peak ages are plausible. For a player like Miller, the model suggests his 3pt shooting ability has been declining since starting his NBA career.
Individual Players
Below you will find graphs of estimated aging curves for some player’s 3FG%. In addition to the estimated aging curve, you will see points plotted that represent the actual 3FG% for the player at the specified age.
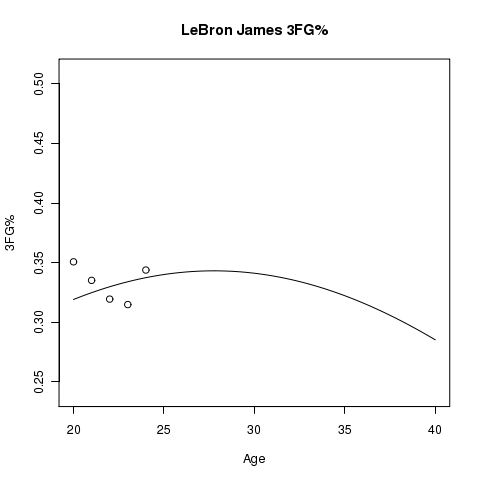
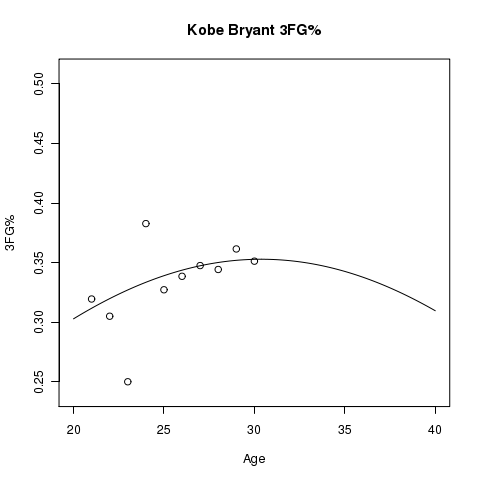
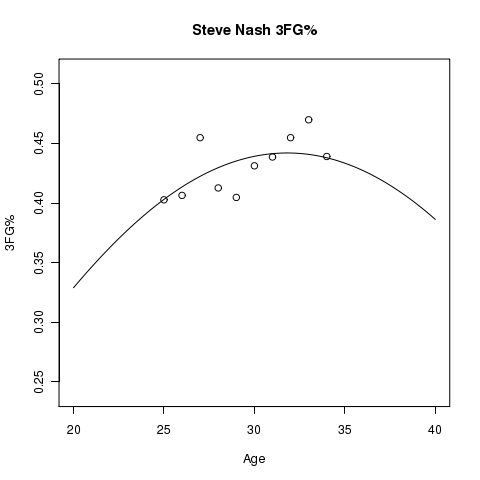
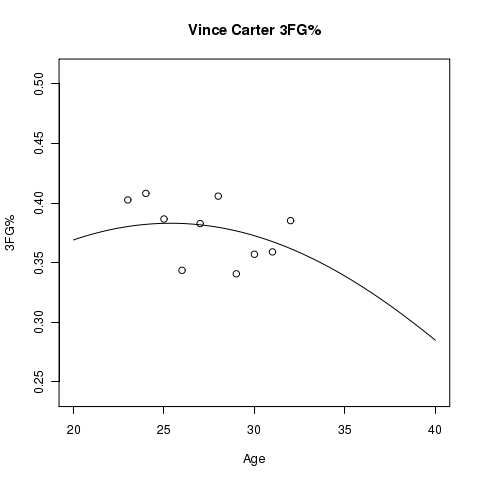
There is Uncertainty…
These are just estimates, and it is important to point out that uncertainty exists around these estimates. I’ve tried to simulate confidence bounds for this model without success, but even though I’m not representing the uncertainty, keep in mind that it does exist.
Improving this Model
The debate in the baseball community suggests it’s incorrect to simply assume players have this type of aging curves. Although this type of curve appears to be a decent approximation, perhaps there are better ways to estimate the impact of a player’s age on 3FG%. Other than trying to control for other explanatory variables, trying to fit other model types might prove worthwhile.
cam girls
[…]Sites of interest we’ve a link to[…]
live sex shows
[…]usually posts some really intriguing stuff like this. If youre new to this site[…]
cam girls
[…]Sites of interest we have a link to[…]
rebirthro
[…]below youll discover the link to some sites that we assume you need to visit[…]
casino en ligne payant
[…]Sites of interest we’ve a link to[…]
unix time to human readable
[…]one of our guests just lately advised the following website[…]
sunrise time
[…]just beneath, are a lot of absolutely not related sites to ours, having said that, they’re certainly really worth going over[…]
maghrib time today
[…]check below, are some completely unrelated websites to ours, having said that, they are most trustworthy sources that we use[…]
current time in different countries
[…]the time to study or visit the material or web pages we have linked to beneath the[…]
time zone converter
[…]very few websites that come about to be detailed beneath, from our point of view are undoubtedly effectively worth checking out[…]
cron to human readable
[…]check below, are some absolutely unrelated sites to ours, on the other hand, they are most trustworthy sources that we use[…]
navkarsi time today
[…]always a massive fan of linking to bloggers that I adore but dont get a lot of link enjoy from[…]
utc time now
[…]Every when inside a even though we select blogs that we study. Listed beneath would be the most recent web-sites that we pick out […]
date of birth calculator
[…]below youll uncover the link to some websites that we consider you need to visit[…]
tron vanity address
[…]Wonderful story, reckoned we could combine a number of unrelated data, nevertheless genuinely really worth taking a look, whoa did 1 find out about Mid East has got much more problerms too […]
tron wallet address generator
[…]please go to the websites we adhere to, which includes this a single, as it represents our picks in the web[…]
tron wallet address generator
[…]Sites of interest we’ve a link to[…]
tron generate address
[…]check below, are some absolutely unrelated web-sites to ours, however, they’re most trustworthy sources that we use[…]
tron wallet address generator
[…]that is the finish of this write-up. Here youll uncover some web pages that we believe youll value, just click the links over[…]
usdt wallet address generator
[…]The details mentioned inside the post are a few of the very best offered […]
doxycycline for sinus infection
doxycycline for sinus infection
vardenafil 20mg price
vardenafil 20mg price
cheap sex webcams
[…]usually posts some extremely interesting stuff like this. If you are new to this site[…]
free nude chat
[…]below youll come across the link to some websites that we think you’ll want to visit[…]
cheap adult webcams
[…]please pay a visit to the web-sites we stick to, which includes this a single, as it represents our picks from the web[…]
cheap antibiotics
cheap antibiotics
live webcam girls
[…]Sites of interest we’ve a link to[…]
Silicon Valley New Construction Homes
[…]one of our guests a short while ago proposed the following website[…]
Northern California Fixer Upper Homes
[…]check below, are some completely unrelated web sites to ours, nevertheless, they may be most trustworthy sources that we use[…]
San Jose Best Real Estate Agent Arpad Racz
[…]here are some hyperlinks to web sites that we link to because we believe they’re really worth visiting[…]
kooky
[…]one of our guests a short while ago advised the following website[…]
tadalafil cialis walmart
tadalafil cialis walmart
restaurants viagra triangle
restaurants viagra triangle
do sildenafil work
do sildenafil work