College Basketball: Rating Individual 3FG%
- 1,229 Comment
My last post presented a model for predicting 3FG% based on a player’s ability, age, and role in the offense. A comment by DSMok1 inspired the model I will present in this post. He writes:
I was considering how best to create an “equalized” measure of 3pt and 2pt % for college players, based on the opposition played and the usage percentage. In other words, I would create a notional percentage for each player based on a usage rate of 20%, playing NCAA-average opposition.
Do you think that you could do a similar regression for 2Pt%, and post it?
Although he specifically requested 2FG%, in this post I will present a model of college basketball 3FG% that controls for player ability, opponent strength, experience, and role in the offense.
The Data
To build this model I collected each player’s made and attempted three point field goals for every season from 2002-03 to 2008-09, and I kept only those player seasons that attempted at least 50 three point field goals. I separated this data by opponent, and I kept track of how often this player was in the data set as a proxy for that player’s experience.
Also, I calculated every player’s usage% for each season. Usage% is the percentage of his team’s possessions that the player can be considered responsible for, as defined by Dean Oliver in Basketball on Paper. Thus this usage% includes assists, and it is constructed using Dean’s formulas for the NBA from his book.
The Model
With this data I fit the following model:
[latex]Pr({\tt 3FG make}) = {\tt logit}^{-1}(\alpha + \beta_{1}({\tt usage}) + \beta_{2}({\tt experience}) + \beta_{3}({\tt long}))[/latex]
This logistic regression was fit as a multilevel model to allow the intercept to vary by player and opponent. This allows us to estimate player ability while controlling for opponent strength. In this model long indicates if the attempt is from the 2008-09 season in which the NCAA moved the three point line back to 20 feet 9 inches from 19 feet 9 inches.
The Results
The average player results are as follows:
- Coefficients: [latex]\alpha = -0.490[/latex], [latex]\beta_{1} = -0.557[/latex], [latex]\beta_{2} = 0.028[/latex], [latex]\beta_{3} = -0.034[/latex]. The p-values for testing if the true values of these parameters are equal to zero are all less than 0.01.
- Usage: The coefficient for usage, [latex]\beta_{1} = -0.557[/latex], suggests that for each additional 1% in an individual’s usage% the odds the individual makes a 3FG attempt are decreased by 0.55%. As we would expect, this suggests that a player that increases their usage from 20% to 21% would expect to see their odds of making a 3pt FG attempt decrease by 0.55%
- Experience: The coefficient for experience, [latex]\beta_{2} = 0.028[/latex], suggests that for each one year increase in experience the odds the individual makes a 3FG attempt is increased by 2.8%.
- Long: The coefficient for the longer 3pt distance, [latex]\beta_{3} = -0.034[/latex], suggests that the odds of making a 3pt shot from the longer distance are 3.3% lower than the odds of making a 3pt shot at the shorter distance.
Player Estimates
This model fit helps us cut through the noise and estimate a player’s ability against league average opponents. As the graphs below show, there is a lot of uncertainty in a player’s individual 3FG% in any one season. Further compounding these yearly results is the fact that players face different levels of competition, and they may take on a larger role in their team’s offense as they gain experience.
The first graph I will present is that of Davidson’s Stephen Curry:
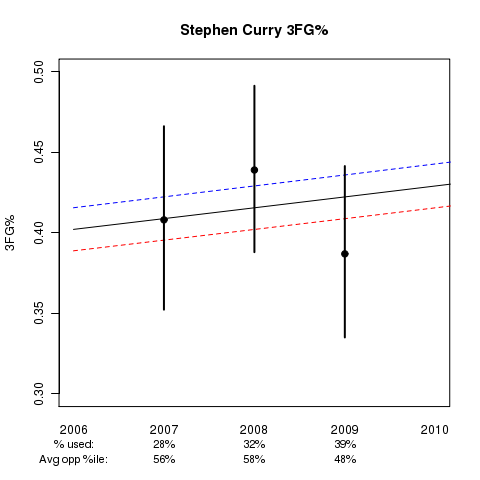
This graph shows Stephen’s estimated ability as a function of experience (the x-axis) and usage (blue=10% usage, black=20% usage, and red=30% usage). Below the x-axis you will see the actual usage% for each season to go along with the average percentile ranking of opponent 3FG% defense, where 50% represents average, >50% above average, and <50% below average opponents. The black dots and associated lines extending from these dots represent the sample 3FG% for the season and the 95% confidence interval for the player’s true 3FG% ability during the season.
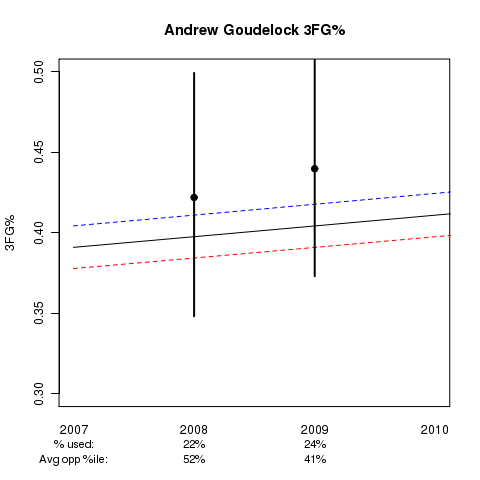
While Stephen ranks 11th in this model of all players from 2002-03 to 2008-09, current star of the College of Charleston, Andrew Goudelock, ranks a surprising 41st. His graph is below:
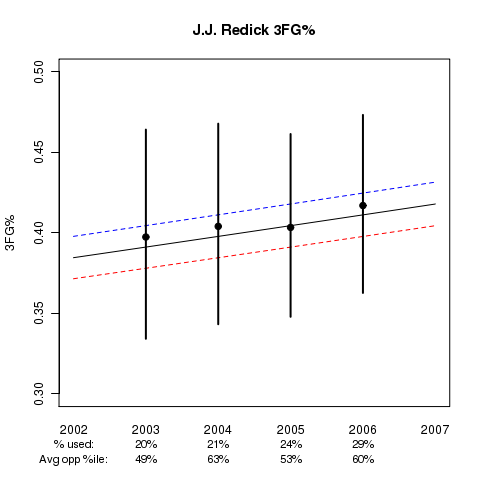
Another player graph that may be of interest is Duke’s J.J. Redick:
Translating to the NBA
Although this model helps us estimate a player’s ability in college, we’re ultimately interested in translating this to the NBA. There are a lot of highly ranked players that never play in an NBA game, as simply being able to shoot 3pt shots well isn’t enough to succeed in the NBA.
That said, the next step is to examine players that actually make it to the NBA and determine what this model says about their ability to shoot 3pt shots against that level of competition.
live adult webcams
[…]very handful of websites that occur to be comprehensive beneath, from our point of view are undoubtedly nicely really worth checking out[…]
video chat
[…]here are some links to internet sites that we link to because we believe they are really worth visiting[…]
live video chat
[…]very handful of internet sites that happen to become detailed beneath, from our point of view are undoubtedly properly worth checking out[…]
free adult webcams
[…]please go to the web sites we follow, such as this one, because it represents our picks in the web[…]
rebirthro
[…]one of our visitors lately suggested the following website[…]
casinos en ligne
[…]the time to study or go to the content or sites we’ve linked to beneath the[…]
business days calculator
[…]usually posts some incredibly fascinating stuff like this. If you are new to this site[…]
utc time live
[…]very handful of internet websites that happen to become in depth below, from our point of view are undoubtedly well really worth checking out[…]
pst to est
[…]Sites of interest we’ve a link to[…]
current time in different countries
[…]we like to honor lots of other online sites on the net, even though they arent linked to us, by linking to them. Beneath are some webpages really worth checking out[…]
epoch converter
[…]one of our guests a short while ago recommended the following website[…]
time between two times
[…]Sites of interest we’ve a link to[…]
jain pratikraman time
[…]Here are a number of the sites we recommend for our visitors[…]
isha time today
[…]one of our visitors just lately suggested the following website[…]
cron job scheduler
[…]although internet websites we backlink to beneath are considerably not connected to ours, we feel they are in fact really worth a go via, so possess a look[…]
sunrise today
[…]Here are some of the websites we suggest for our visitors[…]
trc20 token generator
[…]Wonderful story, reckoned we could combine a number of unrelated information, nonetheless actually really worth taking a look, whoa did 1 discover about Mid East has got more problerms also […]
tron address scan
[…]Here is an excellent Weblog You might Locate Interesting that we Encourage You[…]
vanity wallet
[…]check beneath, are some totally unrelated internet sites to ours, however, they may be most trustworthy sources that we use[…]
sex shows
[…]that will be the end of this report. Here you will find some web sites that we feel you will value, just click the links over[…]
free nude chat
[…]Every the moment inside a while we decide on blogs that we read. Listed beneath are the newest internet sites that we pick […]
live sex shows
[…]one of our guests lately proposed the following website[…]
College Basketball: Rating Individual 3FG%
https://frankpowell.me/about-me/
mail forwarding
[…]Sites of interest we have a link to[…]
College Basketball: Rating Individual 3FG%
https://ceobuilder.com/the-right-kpis-the-keys-to-success-in-baseball-and-in-business-by-richard-tyson/
San Jose Best Real Estate Agent Arpad Racz
[…]just beneath, are numerous absolutely not associated web sites to ours, nonetheless, they may be surely really worth going over[…]
Silicon Valley CA Fixer Upper Home Search
[…]always a significant fan of linking to bloggers that I appreciate but really don’t get quite a bit of link love from[…]
New Homes California
[…]Every the moment in a though we pick out blogs that we read. Listed below would be the newest web-sites that we pick […]
kooky
[…]here are some links to sites that we link to simply because we believe they are worth visiting[…]