The Relationship Between Age, Usage, and 3FG%
- 1,579 Comment
In my last two posts I have taken a look at modeling a player’s 3FG% based on their age, and I’ve also estimated the relationship between usage and 3FG%. In this post I would like to bring these two topics together and estimate the relationship between age, usage, and 3FG%.
The Data
To put this data set together I again used Basketball-Reference.com’s Player Season Finder, but this time I collected the advanced statistics to go along with the player’s 3pt makes and attempts. Also, I used more years of data, as this data set is from the 1989-90 to 2008-09 seasons.
My original threshold for including the player season in the data set was to require at least two 3pt shot attempts during the season. I have, however, increased this threshold to eighty two 3pt shot attempts in an effort to isolate the data set to only players that we expect to shoot 3pt shots. This means that I’m attempting to quantify those players that are “regular” or “semi-regular” 3pt shooters and disregard those that do not consider the 3pt shot a part of their game.
The Model
To estimate the relationship between age, usage, and 3FG%, I’ve fit the following model:
[latex]Pr({\tt 3FG make}) = {\tt logit}^{-1}(\alpha + \beta_{1}({\tt USG\%}) + \beta_{2}({\tt age}) + \beta_{3}({\tt age}^{2}))[/latex]
I fit this logistic regression as a multilevel model to allow the intercept and coefficients for USG% and the age quadratic to all vary by player. This type of model allows us to estimate the player ability while allowing us to estimate individual USG% lines and individual player aging curves.
The Results
The average player results are as follows:
- Coefficients: [latex]\alpha = -1.62[/latex], [latex]\beta_{1} = -0.0061[/latex], [latex]\beta_{2} = 0.081[/latex], [latex]\beta_{3} = -0.00136[/latex]. The p-values for testing if the true values of these parameters are equal to zero are all less than 0.01.
- USG%: The coefficient for usage, [latex]\beta_{1} = -0.0061[/latex], suggests that for each additional 1% in an individual’s USG% the odds the individual makes a 3FG attempt are decreased by 0.6%. As we would expect, this suggests that a player that increases their usage from 20% to 21% would expect to see their odds of making a 3pt FG attempt decrease by 0.6%
- Age: The coefficients for the aging curve, [latex]\beta_{2} = 0.081[/latex] and [latex]\beta_{3} = -0.00136[/latex], suggest that the average player’s peak in 3pt shooting ability occurs when they are 30 years old.
Trevor Ariza
Trevor Ariza was the source of the original motivation for looking at the relationship between usage and 3FG%, so I thought it would be appropriate to present a graph of his estimated aging curve at usage levels of 10% (blue), 20% (black), and 30% (red). The dots represent the sample 3FG% for Trevor at the specified age:
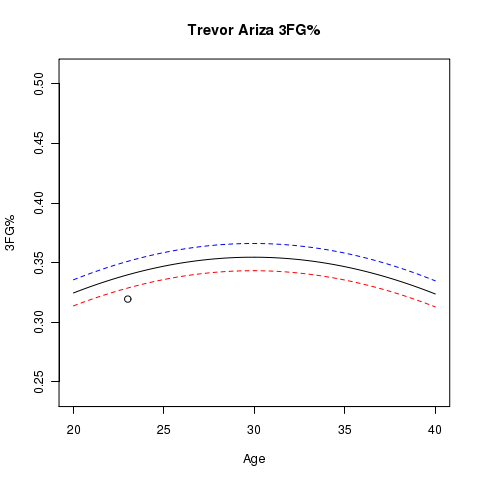
One thing you’ll notice is that we only have one data point on this graph. This is because Trevor did not shoot many 3pt shots until last season with the Lakers.
That said, using just last year’s data for Ariza we would predict him to shoot 34% this year with the Rockets at age 24 using 23.6% of his lineup’s possessions. Thus far this year he’s shooting 34.3%. Don’t read too much into the closeness of this predicted% to his actual%, as a 95% confidence interval for his 3FG% this year is (26.6%, 42.8%).
One thing to note is that this model suggests that last year’s 31.9% performance isn’t a fair representation of his true ability. This model estimates his fair ability of making a 3pt FG attempt to be 34.3% last year with the Lakers at age 23 using 16.7% of his lineup’s possessions.
Other Players
Here are some other player graphs that have more than a single season’s data, where lines for the estimated aging curve at usage levels of 10% (blue), 20% (black), and 30% (red) are shown. The dots represent the sample 3FG% for the players at the specified age:
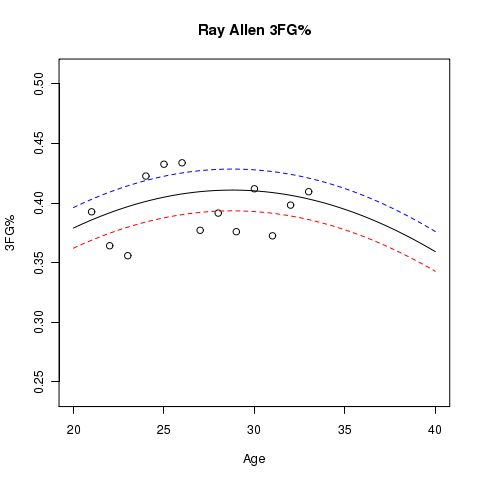
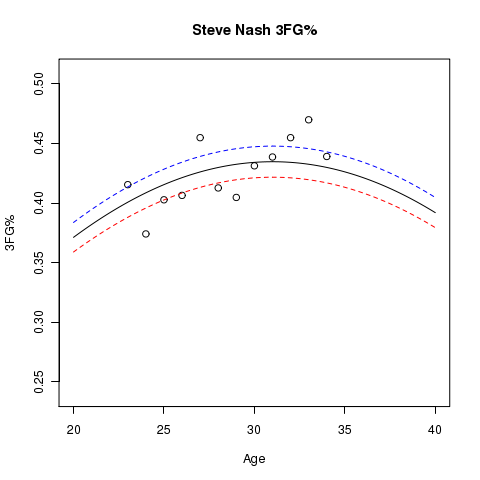
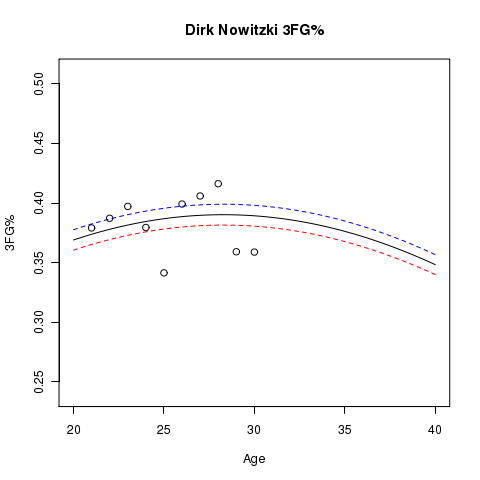
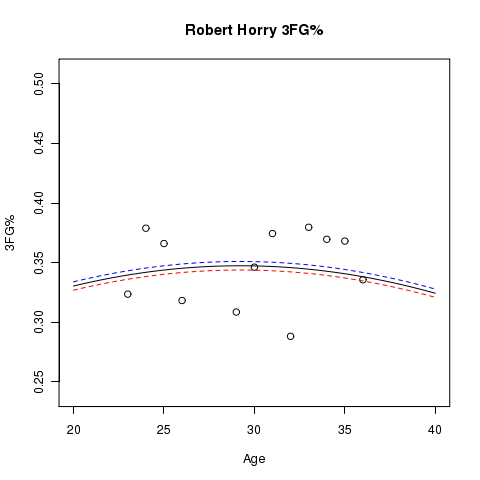
More Work…
The next step is to try and validate these models using out of sample data. One thing I would like to do is to use cross-validation to measure the expected prediction error of this model. Also, I would like to quantify the uncertainty around these estimates. Current efforts to do this have left me unsatisfied, but there are certainly some confidence bounds we could generate for these estimtes, and they should prove to be worthwhile to create.
I’ll have to wait to do this, as my final exams start tomorrow, and I’ve blown off studying for them about as long as I possibly can. 8)
dizain cheloveka
dizain cheloveka
experienceleaguecommunities.adobe.com/t5/user/viewprofilepage/user-id/17937282
experienceleaguecommunities.adobe.com/t5/user/viewprofilepage/user-id/17937282
bento.me/cenforce
bento.me/cenforce
cathopic.com/@levitrasoft
cathopic.com/@levitrasoft
The Relationship Between Age, Usage, and 3FG%
https://legendairymusic.blogspot.com/2019/07/taruhan-bola-resmi-piala-dunia.html
[…] buy cialis pills […]
[…] t 20 pill cialis […]
[…] online cialis prescription […]
[…] how much is cialis […]
[…] viagra sildenafil 50mg tablets […]
[…] sildenafil citrate 25mg tab amazon […]
[…] cialis cheap generic […]
[…] cialis generic cost […]
wix seo experts
[…]Every when in a while we select blogs that we read. Listed beneath are the most recent websites that we pick out […]
wix seo experts
[…]below you will obtain the link to some web sites that we believe you need to visit[…]
youtube-videos
youtube-videos
wix seo specialists
[…]Wonderful story, reckoned we could combine a number of unrelated information, nevertheless genuinely really worth taking a appear, whoa did one study about Mid East has got extra problerms as well […]
wix seo experts
[…]always a massive fan of linking to bloggers that I appreciate but do not get quite a bit of link like from[…]
wix seo specialists
[…]please go to the websites we adhere to, such as this 1, because it represents our picks from the web[…]
The Relationship Between Age, Usage, and 3FG%
https://werepp.com/154-tips-on-avoiding-scotland-tourist-traps/
The Relationship Between Age, Usage, and 3FG%
https://nowejeruzalem.pl/formacja/__trashed-7/
The Relationship Between Age, Usage, and 3FG%
http://varrio-xjew4ux.blogspot.com/2017/07/indo-13-67-street.html
The Relationship Between Age, Usage, and 3FG%
https://churchofhope.com/golfclassic/
The Relationship Between Age, Usage, and 3FG%
https://account.moview.id/login/bW92aWV3/aHR0cHM6Ly9iYXRtYW5hcG9sbG8ucnUvJUQxJTgxJUQwJUJGJUQwJUI4JUQxJTgxJUQwJUJFJUQwJUJBLSVEMCVCNyVEMCVCMCVEMCVCRiVEMCVCOCVEMSU4MSVEMCVCNSVEMCVCOS0lRDAlQkUlRDAlQjElRDAlQkQlRDAlQkUlRDAlQjIlRDAlQkIlRDElOEYlRDAlQjUlRDAlQkM…
The Relationship Between Age, Usage, and 3FG%
https://www.marsonsgroup.com/smoking-to-vaping/
cenforce 200 tablets
cenforce 100mg
extra p force
super p force ervaring
generic drug for imitrex
imitrex and migraines
kamagra chewable
kamagra oral jelly for sale