Practical Unit vs. Unit Efficiency Ratings
In my last post I looked at theoretical unit vs. unit efficiency ratings. Now I will take a more practical look at calculating these ratings.
In the theoretical case we made the assumption that we could know for sure a 5-player unit’s shot distribution, 2pt and 3pt shooting percentages, and turnover and rebounding rates. Clearly, however, this is not the case. In reality we can, at best, estimate these proportions.
Gathering The Data
To estimate these proportions we need data. With this in mind, I wrote an event parser that looks at each unit’s events on a per-play level, and it separates home and away data. This allowed me to pull out actual successes and failures for the shot distribution, shooting percentages, and rebounding rates.
With this data I am able to estimate the true rates for each 5-player unit.
The Model
I have chosen to use Bayesian statistics to model these proportions. For the play distribution (2pt shot vs. 3pt shot vs. turnover), I have used the Dirichlet distribution to model this multivariate proportion. For all other cases, I have used the Beta distribution to model the other proportions.
Also I have used a Uniform prior distribution, so it’s not a good idea to look at 5-player units with small sample sizes, as they miss out on the basic nature of the game of NBA basketball. So this is something that could be improved upon in the future.
An Example Simulation
Now that each proportion is modeled by a distribution instead of being assumed to be known, I have modified the theoretical code to simulate from these distributions so that the uncertainty in the actual proportions is taken into account.
For this example I have used 2007-2008 regular season data from the same units used in the theoretical case: the Celtics unit consisting of Ray Allen, Kevin Garnett, Kendrick Perkins, Paul Pierce, and Rajon Rondo, and the Lakers unit consisting of Kobe Bryant, Derek Fisher, Pau Gasol, Lamar Odom, and Vladimir Radmanovic. Now, however, I have used only the Celtic’s home data and the Laker’s away data.
The Results
The simulation results are:
Celtics Offensive Efficiency: Mean=110.9; SD=12.1
Lakers Offensive Efficiency: Mean=108.9; SD=12.6
Celtics Win%: 54.8%
As would be expected, the Celtic’s 5-player unit at home should be small favorites over the Lakers 5-player unit on the road.
One thing I take away from this result is the importance of the bench. The Celtics aren’t huge favorites with this unit, so the bench clearly has an important role in a game between these two teams. I know, not groundbreaking stuff here, but this result helps to support this classic basketball belief.
Reproduce These Results
These results can be reproduced using this R code: practical_unit_vs_unit.R
To use this code, simply start R and run: source(”practical_unit_vs_unit.R”)
By default 10,000 games of 100 possessions each are run. You can modify the code to change these values by modifying the nsims and nposs variables.
The Next Step
With this practical model in place, there are some areas for improvement.
The first step would be to take into account informative prior distributions for each proportion. Using historical data we should be able to narrow the range of possible values for the true proportion of these events. For example, it’s highly unlikely a 5-player unit’s true offensive rebounding rate is say 50%. Therefore we should be able to narrow the distributions based on the data if we take this sort of common sense into account. This also allows us to get a better handle on units with small samples.
A second area for improvement would be to take each unit’s opponent strength into account, similar to what you might find in a college rating system. Time will tell how large of an issue this would be for a full season’s worth of data, but surely a small sample would garner better results taking opponent strength into account.
This leads into another important area for improvement: the unit vs. unit interaction effects. Using the adjusted for strength data, what is the best estimate of the proportion to expect between these units? My naive method assumes it’s the mean. Clearly this is a lazy approach. How can this be improved?
With all of these things in mind, my next step will be to make each team’s 5-player unit data available on this website so that it can be plugged into the practical code for comparison. I have all of the unit data for the 2007-2008 season, so once that is available the plan is to have the 2008-2009 data update on a daily basis.
Theoretical Unit vs. Unit Efficiency Ratings
So lets say you visit your local magic shop and find a device that will magically give you the true probabilities associated with a 5-player unit’s offensive and defensive performance. You know, the important probabilities associated with things like offensive and defensive field goal percentages, rebounding percentages, and turnover rates.
As cool as it is to have this information, you greedily want more. This is understandable, of course, because you want to know what these 5-player units look like in terms of offensive and defensive efficiency. The answer to your woes? Simulation, of course!
The Basic Model
The basic premise is that you somehow know the distribution of shots and turnovers for each 5-player unit. Also, you know the probabilities associated with making shots and free throws, grabbing boards, and turning the ball over for these 5-player units.
With this information in hand, the simulation of a basic model of a basketball game can be used to analyze offensive and defensive efficiency ratings for two competing units.
An Example
To get an idea of how this works, I used some statistics for the most used 5-player units from the Celtics and Lakers from the 2007-2008 season. The Celtics most used unit consisted of Ray Allen, Kevin Garnett, Kendrick Perkins, Paul Pierce, and Rajon Rondo. The Lakers most used unit consisted of Kobe Bryant, Derek Fisher, Pau Gasol, Lamar Odom, and Vladimir Radmanovic.
Using my data, I crudely approximated various offensive and defensive statistics for these units. These are what I assumed to be the true rates. (Clearly these are not the true rates of these statistics, but they are the best to use to illustrate the idea.)
I then merged these statistics together to obtain the true rate for this matchup. As an example, suppose the Celtics make 50% of their 2pt shots and the Lakers allow their opponents to make 55% of their 2pt shots. Clearly some sort of probability distribution is best suited for estimating the true rate in this matchup, but for this simple theoretical case I simply assumed it is the mean of these two values. Hence the Celtics true 2pt field goal percentage would be (50%+55%) / 2 = 52.5%.
Using these statistics, I simulated 10,000 games between these units. These games were more theoretical in nature, as they simply involved each 5-player unit having 100 possessions each.
The Results
Below are the results from the simulations:
Celtics Offensive Efficiency: Mean=115.5; SD=12.2
Lakers Offensive Efficiency: Mean=115.0; SD=12.5
Celtics Win%: 51.5%
Based on the simulations, this appears to be a fairly even matchup. One area I want to explore is how strategy could help seperate one team from the other. This, however, will require a better model than this one.
Reproduce These Results
These results can be reproduced using this R code: theoretical_unit_vs_unit.R
To use this code, simply start R and run: source(“theoretical_unit_vs_unit.R”)
By default 10,000 games of 100 possessions each are run. You can modify the code to change these values by modifying the nsims and nposs variables.
The Next Step
With this basic model in place, the next step is to take into account the uncertainty associated with estimating the statistics used in the simulation. We can’t know for sure the values of the parameters, but we can estimate them with probability distributions. Simulating from these distributions first will allow us to take this uncertainty into account.
Bridge Jumper Team Projections
Last week Mountain from the APBRmetrics forum updated his projections for the 2008-2009 season based on 10% of games being played. This made me wonder what a bridge jumper’s projections would look like. For this case, I define a bridge jumper as someone who ignores all historical data and believes that only data from this season is relevant. He also doesn’t care that the Wizards will get Arenas back at some point this season, so he doesn’t take these kinds of impacts into account.
The Method
A few months ago when I created a graphical representation of the perfect score, I found that using a team’s margin of victory instead of points scored and allowed seemed to be a good approximation for the bell curve method.
Therefore, I take each team’s margin of victory, separating home and away games, and I calculate some statistics. These calculations provide me with a mean and sample standard deviation for each team’s home and away margin of victory distribution.
I then use these distributions to calculate each team’s probability of winning each of their remaining games. This probability is calculated by creating a new normal random variable that is the difference between the home and away team’s normal random variables.
With these probabilities in hand, I add the team’s actual wins to their expected wins for the remainder of the season. For each remaining game, the team’s expected win amount is simply their probability of winning, since each game is simply a bernoulli trial.
The Results
Below are the results through last night’s games. Over the next couple of days I plan on updating this on a daily basis. Also, I plan on simulating the season using this method in an attempt to calculate playoff odds similar to Hollinger’s Playoff Odds. Until then, here are the projections:
Western Conference
1 64.14 Los Angeles Lakers
2 52.20 Utah Jazz
3 51.39 Houston Rockets
4 48.77 Phoenix Suns
5 47.44 Denver Nuggets
6 47.02 New Orleans Hornets
7 44.97 Portland Trail Blazers
8 40.57 Golden State Warriors
X 39.21 San Antonio Spurs
X 34.24 Sacramento Kings
X 33.77 Dallas Mavericks
X 29.89 Memphis Grizzlies
X 27.57 Minnesota Timberwolves
X 19.23 Oklahoma City
X 13.25 Los Angeles Clippers
Eastern Conference
1 56.05 Cleveland Cavaliers
2 52.56 Boston Celtics
3 51.23 Orlando Magic
4 49.44 Atlanta Hawks
5 47.05 Detroit Pistons
6 46.72 Miami Heat
7 43.00 Philadelphia 76ers
8 42.79 New York Knicks
X 42.47 Indiana Pacers
X 41.62 Toronto Raptors
X 39.08 Milwaukee Bucks
X 36.16 New Jersey Nets
X 36.06 Chicago Bulls
X 28.05 Charlotte Bobcats
X 24.06 Washington Wizards
Special thanks to Doug’s NBA Stats for providing game results in an easy to parse format.
Now Updated Daily: 2008-2009 Play-By-Play Data
Play-by-play data for the 2008-2009 regular season is now available and will be updated on a daily basis. For more details, visit the data page. To go straight to the data where you can download a ZIP archive or data from an individual game, visit the 2008-2009 download page.
The Format
This data is in a CSV format like the data I released for the 2007-2008 regular season, which means it has on-court player information as well as shot location information.
There are two reasons for this CSV format. First, I want to make parsing the data as easy as possible so that the number of people capable of doing basketball research will grow. Which means the number of people interested in play-by-data will grow. Hopefully this means the number of people interested in squeezing the last rusty nugget from box score data will diminish.
Also, this CSV format is used to encourage people like you to track data. If you have an interest in keeping track of a stat you can’t get anywhere else, then simply add a new column to the CSV and track it. If you’d like to share your data, please contact me by e-mail: ryan@basketballgeek.com.
Missing Data
There will be some missing games due to data problems that do not allow me to aggregate the data in the CSV format I want publish. Therefore, vist basketballvalue.com if you are in need of a more complete archive.
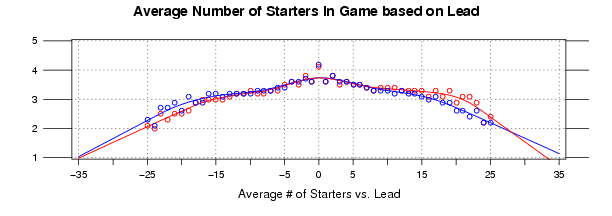
The Average Number of Starters Based on Lead
Now that I’ve looked at how the average number of starters changes based on time, I want to take a look at how this statistic changes based on a team’s lead (or deficit).
The ultimate goal from all of this is to model realistic substitution patterns over the course of a game, as this is important for a realistic simulation. Therefore, I am hoping that this problem will be easier to tackle after looking at these general models of how the average number of starters changes based on game situation.
The Data
To create this basic model, I went through the 2007-2008 regular season play-by-play data and kept track of two things: the home team’s lead (or deficit) and the number of starters in the game for each team. These data points were taken at one minute intervals from the start of the game (0 minutes elapsed) to one minute remaining (47 minutes elapsed). Also, I stripped out anything less than -25 and greater than 25 due to the unrealistic shapes they were forcing into the splines.
My next post will make an attempt at modeling the average number of starters based on elapsed time and lead, so I selected this data collection method so that this joint distribution of elapsed time and lead can be related back to this post and the previous post.
The Model
The graph below illustrates the data:
Click Image for Full Size
In the graph above, the y-axis, from 5 to 1, is the average number of starters in the game based on the team’s lead (or deficit). The x-axis, from -35 to 35, represents the lead (negative numbers represent a deficit). The blue dots and lines represent the home team, and the red dots and lines represent the away team. The lines are drawn from smoothing splines that I fit with R for each team.
So for any given time in the game, the average number of starters decreases based on the number of points a team is leading (or trailing) by. Thus you’re going to, on average, see more starters in the game when the game is close. This shouldn’t be ground breaking news to anyone, but this should give a good visual representation of how the average number of starters varies based on a team’s lead.
One thing I find interesting is that teams still average roughly 2 starters when the game is a blowout. I suspect this result has something to do with when this high margin is taking place early in the game (say before the 4th quarter), so I’m interested in seeing how the average changes when taking into account the elapsed time and the lead.
Reproduce These Results
In this archive you will find the data and R code I used to create the graph above and the smoothing splines fit to the data.
To run the code: extract the archive, open R, and run: source(”starters.R”)
The Next Step
In my last diversion (for now) into how the average number of starters changes in an NBA game, I will make a basic model that takes into account both elapsed time and lead. This should prove useful when trying to understand exact substitution patterns, but it should also prove useful when looking at how other statistics change based on elapsed time and lead.