Basketball Geek
Advancing our understanding of the game of basketball

I’ve been lucky enough to take part in an independent study with my advisor this semester, where I study various methods for ranking things, like sports teams. Our specific area of application is the NCAA tournament, but these methods can be used for much more.

My main interest is in how to apply ranking methods to various NBA statistics at the team, unit, and player level. I am initially focusing on ranking various team statistics such as efficiency, rebounding%, shooting% from various spots on the court, TOs per possession, etc. Over time I will make the daily ratings available in a stats section on this website, but for now I’ll just post the results as I get the rankings together.

My first application is to net efficiency ratings, where a team’s net efficiency rating is their offensive points per 100 possessions – defensive points per 100 possessions.

To rank and rate the team’s net efficiency ratings, I have used Kenneth Massey’s linear regression method outlined in his paper Statistical Models Applied to the Rating of Sports Teams.

The implementation I used adjusts for the team’s strength of schedule and measures home court advantage. As of this writing, the home court advantage was measured to be worth 3.20 points per 100 possessions.

The Ratings

The chart below shows each team’s adjusted net efficiency rating next to their actual net efficiency rating (unadjusted). The usefulness of this is debatable, as the differences between the adjusted and unadjusted ratings is fairly small. There are some switches in rank here and there (such as ORL over LAL), but the conclusions you draw about the teams based on their adjusted versus unadjusted ratings aren’t likely to change much.

Rank	Team	Adjusted Rating	Unadjusted Rating	Rank	Team	Adjusted Rating	Unadjusted Rating
1	CLE	10.91	11.56	16	MIL	0.43	0.37
2	BOS	10.07	10.77	17	DET	-0.79	-0.10
3	ORL	7.69	8.16	18	IND	-1.09	-2.12
4	LAL	7.58	8.81	19	TOR	-1.87	-2.46
5	POR	4.19	4.14	20	CHA	-2.28	-2.77
6	NOH	3.62	3.60	21	NYK	-2.52	-2.50
7	DEN	3.58	3.83	22	CHI	-2.59	-2.85
8	HOU	2.95	3.21	23	MIN	-3.13	-2.98
9	SAS	2.51	3.59	24	GSW	-4.36	-4.56
10	PHX	1.87	2.21	25	NJN	-4.80	-3.80
11	UTA	1.78	2.88	26	OKC	-7.03	-6.27
12	ATL	1.47	1.80	27	WAS	-7.40	-8.34
13	PHI	0.99	0.77	28	MEM	-7.94	-7.07
14	DAL	0.84	1.21	29	LAC	-8.70	-8.91
15	MIA	0.45	1.08	30	SAC	-9.62	-10.22

Making Predictions

This method assumes each possession deserves equal weight. If we assume that this is a fair way to rate a team’s net efficiency for future predictions, then we can make predictions with the following formula:

margin = home team rating + home court advantage – away team rating

Where margin is the net number of points we expect the home team to win by per 100 possessions played. So if Cleveland is hosting the Celtics, we expect Cleveland’s margin to be 10.91 + 3.20 – 10.07 = 4.07 points per 100 possessions. If Boston is instead hosting the Cavs, then we expect Boston’s margin to be 10.07 + 3.20 – 10.91 = 2.36 points per 100 possessions.

Summary

These ratings give us a better sense of a team’s actual net effeciency rating with respect to the entire league, but as you can see from the chart the differences are, in most cases, not that large and have only a small impact on the actual rank of each team.

This is the first part of a four part series in which I will examine how a player’s shooting percentage at each position is a function of the player’s age, height, and weight. This is a four part series because I will be examining four locations on the court: the low paint, the high paint, mid-range jump shots, and 3pt shots.

Below is background information that will apply to all four parts of this series:

Background: The Data

• Shot locations: For this study I divided the court into 4 distinct areas:

1. Low Paint: The area in the paint that is within 6 feet of the hoop.
2. High Paint: All other area in the paint.
3. Mid-Range: All other 2 point shots.
4. 3pt Shots: All 3 point shots.

• Position: A player’s position as designated by by Doug’s stats raw player data, where the positions are PG for point guards, SG for shooting guards, SF for small forwards, PF for power forwards, and C for centers. For clarity, I hold each player’s position constant for every season.
• Age/Height/Weight: A player’s age, height, and weight was constructed using the players.csv file from Database Basketball’s stat download. All ages are as of October 1st of each year, heights are in terms of feet, and weights are in terms of pounds.
• Makes and Misses: A player’s makes and misses from each location come from the 2002-2003 to the 2007-2008 seasons. Thus shot information from 6 seasons were used.

Background: The Method

To fit the data, I used Ed Küpfer’s aging work and Jim Albert’s book Bayesian Computation with R as a guide. For each shot location and position combination, I fit a logistic regression to understand how a player’s age, height, and weight impact a player’s probability of making shots from each location.

So to use the model fit, you need to run logit^-1(x), where x is the model fit, and the inverse logit is defined as: logit^-1(x) = e^x / ( 1 + e^x )

Location #1: The Low Paint

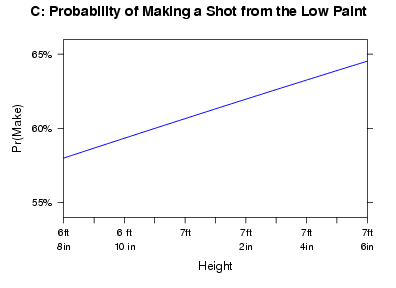
Point Guards

Age: Age is not an indicator of a point guard’s chances of making shots at this location of the court. For point guards, age should certainly affect their explosiveness and ability to get shots from this area of the court (something worth studying in the future), but once they are there to attempt a shot, age does not alter what we would expect out of the players probability of then making that shot.

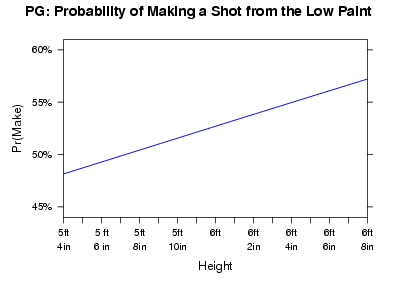
Height: Height, however, is a much different story. As one might expect, height reigns supreme from this area of the court. There is a clear impact, as we would project the tallest point guard in this data set, with a height of 6′ 8″, to make close to 8.5% more shots from this area of the court compared to the smallest point guard in this data set, with a height of 5′ 5″.

Weight: Weight alone has a positive impact, but it is relatively small. This impact can be fully explained by height, as there is a positive correlation between height and weight. Thus knowing a point guard’s height makes the weight data unnecessary.

The Fit: Based on the results above, height (out of age, height, and weight) is clearly the way to project a point guard’s probability of making a shot from this location on the court.

Intercept	Std. Error	Height	Std. Error
-1.5310	0.2685	0.2732	0.0434

Graph: The graph below shows how a point guard’s probability of making a shot from the low paint changes based on the point guard’s height.

Shooting Guards

Age: Like point guards, age does not tell us much with respect to shooting guards. I can actually fit a reverse curve to this data when only using age, but that would mean players are really good when they are young, decrease in ability until the middle of their career, and then raise their performance when they get older. This fit has to do with outliers (where only the “best” players are playing at these young and older ages), thus I do not consider this a representative fit. This is shown when fitting height, as this reverse age curve goes away.

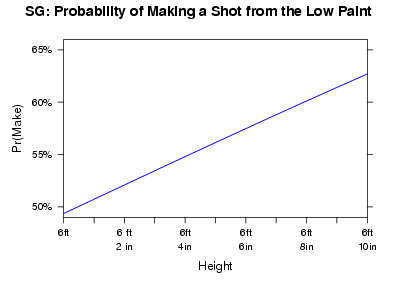
Height: No surprise here, as height again helps explain a lot. In this case, we would expect the tallest shooting guard in this data set, with a height of 6′ 9″, to make almost 10% more shots from this area of the court compared to the smallest shooting guard in this data set, with a height of 6′.

Weight: Weight alone has a positive impact, but again that has to do with the correlation between height and weight. What is different here, however, is that when you combine height and weight, an increase in weight means a decrease in shooting percentage.

This is interesting to me, but taking a closer look at an example helps shed some light into this. A shooting guard is more likely to rely on quickness to get into this area of the court to shoot, so a heavier player at the same height is likely going to lose some quickness when compared to a lighter player. I’m sure there are other explanations that make basketball sense, too.

For example: In this data set, there are 13 shooting guards that are 6′ 7″ tall and weigh anywhere from 244 pounds to 185 pounds. Using the height and weight fit, the heaviest player for this height at 244 pounds is expected to make 2% less of their shots than the player weighing 185 pounds. This is not a huge difference considering the 59 pound weight difference, but this makes sense to me. Thus a combination of height and weight gives us a better picture than simply height alone.

The Fit: Based on the results above, height and weight (out of age, height, and weight) are the best ways to project a shooting guard’s probability of making a shot from this location on the court.

Intercept	Std. Error	Height	Std. Error	Weight	Std. Error
-3.642	0.3747	0.6532	0.0686	-0.0014	0.0006

Graph: The graph below shows how a shooting guard’s probability of making a shot from the low paint changes based on the shooting guard’s height.

Small Forwards

Age: For small forwards, a classical aging curve can actually be fit to this data. As Albert shows in his book on page 248, the peak age can be found with this fit, and for this position it is at age 27. The peak age is defined to be (on average): -agec / ( 2 x agec² ), where agec is the age coefficient and agec² is the age squared coefficient.

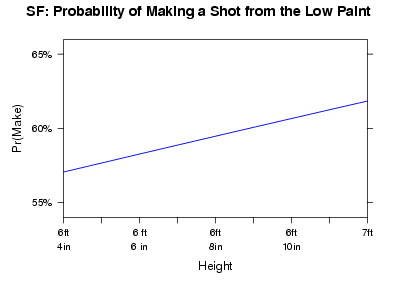
Height: Height again has a positive impact. Holding the ages constant, we would expect the tallest small forward in this data set, with a height of 7′, to make 3.5% more of their shots than the smallest small forward in this data set, with a height of 6′ 4″.

Weight: Like shooting guards, when holding age and height constant, weight has a negative impact on a player’s probability of making a shot. This is a relatively small impact, but it seems to make sense as in the case of shooting guards, so it’s best to leave this coefficient in place.

The Fit: Based on the results above, age, height, and weight all impact a small forward’s probability of making a shot from this location on the court.

Intercept	SE	Age	SE	Age2	SE	Height	SE	Weight	SE
-2.9660	0.4727	0.1245	0.0214	-0.0023	0.0004	0.2978	0.0555	-0.0014	0.0005

Graph: The graph below shows how a small forward’s probability of making a shot from the low paint changes based on the small forward’s height.

Power Forwards

Age: Like the guards, age does not tell us much about a power forward’s probability of making a shot from this location on the court.

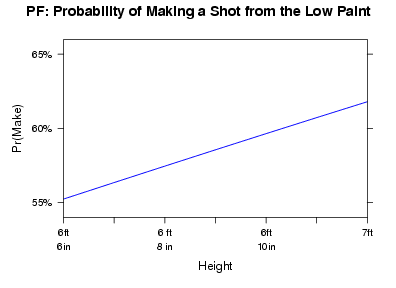
Height: Again, no surprise here, but taller power forwards are more likely to make shots from this location on the court than shorter ones. We would expect the tallest power forward in this data set, with a height of 7′, to make 4.5% more of their shots than the smallest power forward in this data set, with a height of 6′ 7″.

Weight: For the power forward, weight has a positive impact on the probability of making a shot from this location on the court, even when taking height into account. This makes sense when thinking about the role of these players, as a stronger, heavier player is more likely to get better position to create a higher percentage shot.

The Fit: Based on the results above, height and weight (out of age, height, and weight) are the best ways to project a power forward’s probability of making a shot from this location on the court.

Intercept	Std. Error	Height	Std. Error	Weight	Std. Error
-3.8582	0.4931	0.5413	0.0683	0.0022	0.0004

Graph: The graph below shows how a power forward’s probability of making a shot from the low paint changes based on the power forward’s height.

Centers

Age: As with all positions except for the small forward, age does not tell us much about a center’s probability of making a shot from this location on the court.

Height: The theme for this location on the court is height, and it again shows a positive impact with the center position. We would expect the tallest center in this data set, with a height of 7′ 5″, to make 7% more of their shots than the center with the smallest height in this data set, with a height of 6′ 9″.

Weight: Like the power forward, weight has a positive impact on the probability of making a shot from this location on the court.

The Fit: Based on the results above, height and weight (out of age, height, and weight) are the best ways to project a center’s probability of making a shot from this location on the court.

Intercept	Std. Error	Height	Std. Error	Weight	Std. Error
-2.404	0.4224	0.3310	0.0639	0.0020	0.0004

Graph: The graph below shows how a center’s probability of making a shot from the low paint changes based on the center’s height.

Summary

Size matters in this area of the court. The taller you are, the better your expectation is on making a shot. Age and weight are a mixed bag, with age really not telling us too much (with the exception of course being the small forward, although this effect is still small). Weight can help explain some change, but it is not a huge impact regardless.

One thing to stress is that a player must still fit the mold of this position to be successful. Height certainly matters, but height doesn’t mean a shooting guard has the ability to isolate a defender and make their way to the hoop. Thus it’s important to keep in mind that this is simply part of the overall picture.

Taking into account opponent strength is one area I continually question when studying all forms of NBA statistics, whether it be at the team, 5-player unit, or individual player level. Having the ability to quantify this is something I want to get a handle on, so I’ve spent time studying methods the BCS uses to rank college football teams. More specifically, I have studied the Colley Matrix Method created by Wes Colley.

I feel I have a strong understanding of how the method works, so my first application will be to a team’s 3pt shooting statistics. I’m still studying how to quantify the uncertainty in the method, so while I have a belief as to how to measure this uncertainty I will leave that for a future time until I’ve got a firmer grip on what I believe to be true.

The Method for Rating 3pt Shooting Statistics

To setup the Colley matrix, I create 60 “teams”: one “team” for each team’s offensive 3pt shots attempted, and one team for each team’s defensive 3pt shots faced.

So an offensive team’s “wins” are the number of 3pt shots made, and the number of offensive team’s “losses” are the number of 3pt shots missed. The reverse is true for defensive team’s “wins” and “losses”.

In addition to the Colley matrix, the b vector is created using the win-loss information as outlined above.

Solving for the Ratings

To solve for the ratings (the r vector), one must solve:

r = C^-1 x b

Solving this equation gives you the ratings for each team.

The Results

Below are the offensive and defensive ratings using data from all games of the 2008-2009 season played on or before December 23rd:

Offensive Ratings

Rank	Team	Rating	Rank	Team	Rating	Rank	Team	Rating
1	SAS	0.4681	11	ATL	0.4437	21	MEM	0.4167
2	PHX	0.4664	12	OKC	0.4430	22	MIA	0.4100
3	NOH	0.4627	13	TOR	0.4425	23	UTA	0.4081
4	POR	0.4586	14	ORL	0.4423	24	DAL	0.4014
5	BOS	0.4544	15	CHA	0.4386	25	WAS	0.3994
6	DET	0.4522	16	DEN	0.4349	26	GSW	0.3941
7	LAL	0.4504	17	NYK	0.4334	27	SAC	0.3824
8	HOU	0.4495	18	IND	0.4235	28	LAC	0.3813
9	CHI	0.4456	19	CLE	0.4229	29	MIN	0.3783
10	NJN	0.4450	20	MIL	0.4191	30	PHI	0.3642

Defensive Ratings

Rank	Team	Rating	Rank	Team	Rating	Rank	Team	Rating
1	ATL	0.6070	11	DET	0.5883	21	TOR	0.5611
2	BOS	0.6070	12	PHI	0.5847	22	CHA	0.5603
3	NYK	0.6066	13	UTA	0.5820	23	OKC	0.5588
4	HOU	0.6028	14	LAC	0.5800	24	MIA	0.5538
5	DAL	0.6016	15	LAL	0.5794	25	MEM	0.5462
6	MIL	0.6002	16	SAS	0.5715	26	POR	0.5405
7	CHI	0.6001	17	IND	0.5690	27	MIN	0.5370
8	DEN	0.5939	18	WAS	0.5683	28	GSW	0.5323
9	ORL	0.5935	19	PHX	0.5643	29	SAC	0.5119
10	CLE	0.5891	20	NOH	0.5641	30	NJN	0.5117

Using These Ratings

One noteworthy aspect of the Colley Matrix Method is that the mean rating is 0.5. Thus you can interpret these ratings in terms of “against 0.500 level competition”. This means the log5 method can be used to calculate expectations for any given matchup.

For example, suppose the Boston Celtics play the Golden State Warriors. What % of 3pt shots should we expect the Celtics to make? The Warriors?

Applying the log5 method:

The Celtics Expectation Is

0.4544 x (1-0.5323) / ( 0.4544 x (1-0.5323) + (1-0.4544) x 0.5323) = 0.423 = 42.3%

The Warriors Expectation Is

0.3941 x (1-0.6070) / (0.3941 x (1-0.6070) + (1-0.3941) x 0.6070) = 0.296 = 29.6%

Future Work with the Colley Matrix Method

Applying the Colley Matrix Method to team level 3pt shooting statistics is mainly just to help show how this might be applied to other areas of basketball statistics. I am most interested in applying this to 5-player unit level statistics, with the ideal goal of using those to extract each player’s impact.

Where would you like to see the Colley Matrix Method applied?

If you are reading this post then you are undoubtedly familiar with the increased popularity of plus/minus and adjusted plus/minus ratings. These methods help account for a player’s contributions made while he is on the court that are not measured by traditional statistics.

Thanks to the work done by the likes of Dan T. Rosenbaum, David Lewin, Steve Ilardi, Aaron Barzilai, and Eli Witus, adjusted plus/minus has become the standard for measuring a player’s on-court contributions. Thus we can be sure that adjusted plus/minus is the best available method to measure a player’s on-court contributions.

The Motivation to Create Something New

So, then, why create something new if adjusted plus/minus already exists?

It is because my motivation comes from the fact that I have a hard time interpreting adjusted plus/minus. The way the data is fit does not seem “clean” to me, although I suspect my reservations in this area come from rare cases that probably don’t affect the ratings very much. Also, to be honest, this motivation likely comes from my level of statistical ability when compared to those mentioned above. I am not at their level, so I need something, perhaps more basic, that makes sense to me.

Therefore, my goal was to create something that I could interpret, since having a way to measure a player’s overall contributions to his team is very important. I think we have way too many ways to rate players as it is, but the most important one to me, adjusted pus/minus, I can’t explain.

I don’t suspect I have the ability to compete with PhDs, so it is safe to say that adjusted plus/minus has a better foundation than my method. That said, I feel I now have a measurement that I can actually explain to someone with respect to a player’s overall on-court contributions.

The Theory of Points Added

The theory of points added is that the points scored on any given possession can be explained by the following formula:

Points = O1 + O2 + O3 + O4 + O5 + D1 + D2 + D3 + D4 + D5

Where O1,…,O5 and D1,…,D5 stand for the offensive and defensive players, respectively.

The idea is that every player adds something to the points on a given possession. This is different from a plus/minus viewpoint, since no player has negative contributions. (You can’t have negative points scored, can you?) Thus the best offensive players have a larger number of points added, and the best defensive players have a small number of points added.

The Method for Fitting the Data

With the basic theory in place, I chose to use the following formula for fitting the data:

Points = HCA + O1 + O2 + … + ON + D1 + D2 + …  DN

I have suppressed some details, so let me explain. First, the intercept for this equation is forced to be 0. The HCA variable measures the home court advantage. It exists in the formula if the offensive team is at home. Thus it does not exist otherwise. For the N number of players measured, O1,…,ON measures the points added on offensive possessions for each player, and D1,…,DN measures the points added on defensive possessions for each player. It is worth noting that for any given data point (as represented by the points scored on any given possession), only 5 offensive and defensive players are on the court. Thus all other players do not exist in the formula when fitting any given data point.

Fitting 2007-2008 Data with WinBUGS

I chose to use WinBUGS to fit the data for a couple of reasons. First, WinBUGS allows me to restrict the data in the logical form I wish to fit. Thus when sampling from the Normal distribution when fitting the data, I am able to limit these points to be strictly positive. The other reason for using WinBUGS is that the dimensionality of the data can be reduced thanks to the way the models are specified. This means that instead of trying to fit 216MBs of data, I can instead fit 6MBs of data. (My Mac especially appreciates this.)

To fit this model, you will need a couple of files: the model specification, pa_linear.bug; the R code needed to call WinBUGS from R, pa_linear.R; and the possession data, PA.bugs.data (which is in ZIP format, so you must extract it before use). You will need the R package R2WinBUGS to call WinBUGS from R. Also, you will need to update the wbugs_dir (and wine/winepath if on a UNIX box) variables in pa_linear.R for your environment. Lastly, you should grab 07-08.players.ids to match up the player’s ID numbers with their actual names.

The Results

If you use the R code to run WinBUGS for fitting the model then you should end up with a file log.txt that has the estimated coefficients to fit the data, along with their standard deviations and 95% credible intervals for the fits.

To clean up the data, I have extracted each player’s offensive and defensive points added per possession and transformed them in terms of 100 possessions to create points added offensive and defensive ratings.

Note: The data is only for the top 75% of players with respect to the total number of offensive and defensive possessions. Also, home court advantage was measured to be roughly 4.19 points per 100 possessions, with a standard deviation of 0.57 points per 100 possessions.

The top 10 offensive players of 2007-2008 are:

Player		Mean		Std. Dev.
Steve Nash		23.98		3.75
Chris Paul		21.81		4.62
Dwyane Wade		21.77		3.34
C.J. Miles		21.03		4.22
Kobe Bryant		20.80		4.40
Dwight Howard		20.43		7.20
Devin Harris		19.77		2.95
Kevin Martin		19.46		3.23
Sasha Vujacic		18.40		3.95
Jamario Moon		18.40		3.62

The bottom 10 offensive players of 2007-2008 are:

Player		Mean		Std. Dev.
Jermaine O’Neal		2.52		2.00
Yi Jianlian		2.62		2.14
Johan Petro		2.67		2.03
Jason Collins		3.00		2.17
Nenad Krstic		3.04		2.44
Kwame Brown		3.04		2.33
Kris Humphries		3.06		2.48
Robert Horry		3.27		2.55
Jameer Nelson		3.54		2.94
Mark Blount		3.63		2.47

The top 10 defensive players of 2007-2008 are:

Player		Mean		Std. Dev.
Kevin Garnett		2.08		1.72
Joel Przybilla		2.32		1.89
Nenad Krstic		2.42		1.92
Rasheed Wallace		2.66		2.17
Jason Collins		2.87		2.12
Josh Smith		3.05		2.17
DeSagana Diop		3.05		2.26
Chuck Hayes		3.08		2.27
Shaquille O’Neal		3.13		2.15
Sasha Pavlovic		3.23		2.29

The bottom 10 defensive players of 2007-2008 are:

Player		Mean		Std. Dev.
Sasha Vujacic		25.45		3.96
Al Jefferson		23.22		4.37
Chris Paul		22.70		4.19
Andre Miller		21.29		4.20
Marcus Williams		21.03		3.98
Jose Calderon		20.98		5.09
Acie Law		19.97		5.13
Carlos Arroyo		19.74		4.77
Ben Gordon		19.45		3.01
Mike Bibby		19.24		3.69

For all of the ratings, see the offensive ratings document and the defensive ratings document.

Conclusions

We have to be careful drawing conclusions from these ratings, specifically since they are only for a single season of data and have the typical issues that adjusted plus/minus has with respect to a small sample. Also, it is worth remembering that the performance of players can be affected by their role/coaching/etc. This model does not try and control for these factors, as it simply controls for home court advantage and the other players in the league.

Summary

My hope is that these will be useful with respect to looking at a player from a broader perspective. We don’t have great ways to measure defense, but hopefully this helps in the same manner as adjusted plus/minus does.

I’d like to hear any comments or criticisms of the methodology, especially since adjusted plus/minus has become widely used. Of course I find points added easier to understand and feel it is “cleaner”, but I also don’t have a PhD. 🙂